Công Thức Tính Diện Tích Tam Giác Thường, đều, Vuông, Cân Chuẩn

Ngay từ những ngày học cấp tiểu học, chúng ta đã được tiếp xúc và học các chương trình Toán học về hình học, cụ thể là tam giác. Về sau khi đi sâu vào phọc phần Toán hình thì chúng ta càng được trau dồi những kiến thức rộng lớn hơn.

Trong Toán hình học gồm có tam giác vuông, tam giác đều và tam giác cân,… Vậy để giúp mọi người biết chính xác Công Thức Tính Diện Tích Tam Giác Đều, Vuông, Cân kèm theo những ví dụ cụ thể để dễ hiểu và áp dụng tốt nhất, hãy cùng blog Pixwares xem bài viết này dưới đây:

Trong toán học có những loại tam giác nào?

Để vận dụng đúng công thức tính diện tích hình tam giác, trước hết bạn cần xác định đó là loại tam giác gì? Sau khi xác định được chính xác rồi, bạn có thể tính đúng và chính xác diện tích hình tam giác mà câu hỏi đưa ra.

Có nhiều dạng tam giác khác nhau trong toán học, và được chia ra như sau:

• Hình tam giác có góc nhọn nhỏ hơn 90 độ
• Tam giác bình thường
• Tam giác vuông góc
• Tam giác đều
• Hình tam giác có góc tù lớn hơn 90 độ
• Tam giác cân
• Tam giác vuông

Công thức tính diện tích hình tam giác đúng

Công thức tính diện tích hình tam giác lớp 10 là phần kiến ​​thức hình học mà các em sẽ cần trang bị cho mình. Những kiến ​​thức này là nền tảng và rất quan trọng để có thể giải các bài toán sau này.

Hãy cùng chúng tôi sưu tầm các công thức tính diện tích tam giác đều, hình vuông, tam giác đều, tam giác cân, tam giác vuông

Công thức tính toán diện tích tam giác thường

Định nghĩa

Một tam giác bình thường là một tam giác có các cạnh có độ dài và góc khác nhau và có các số đo khác nhau. Cho ABC là tam giác có ba cạnh là a, b, c và chiều cao ha, như hình bên:

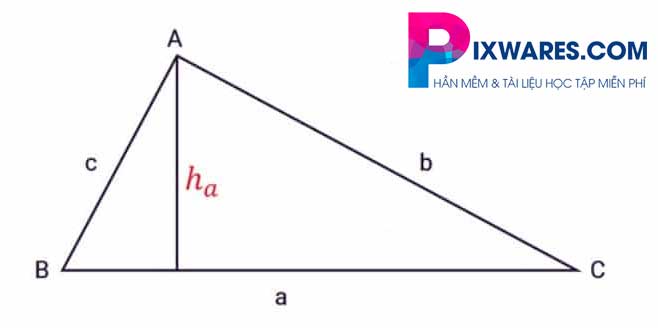
Công thức tính chu vi tam giác thường

Đối với một tam giác bình thường, chu vi của nó bằng tổng độ dài ba cạnh của tam giác. Công thức cụ thể là:

P = a + b + c

trong đó: P là chu vi của tam giác. a, b, c là các cạnh của tam giác đó.

Công thức tính diện tích tam giác thường

Diện tích của một tam giác thường bằng 1/2 tích độ dài của cạnh đối diện với chiều cao của đỉnh đối với cạnh đối diện.

S = 1 / 2a.ha = 1 / 2b.hb = 1/2 c.hc

Ví dụ: Tính diện tích hình tam giác có chiều dài 4m, chiều cao 20dm.

Sau đó, chúng tôi giải quyết nó theo công thức chung sau:

Thay đổi chiều cao của tam giác thành 20dm = 2m.

Diện tích hình tam giác được tính như sau:

S = (4 × 2) / 2 = 4 mét

Vậy diện tích của hình tam giác là 4 mét

• Công thức tính diện tích tam giác khi biết một góc

Khi biết một góc, diện tích tam giác sẽ bằng 1/2 tích của hai cạnh kề sin của góc tạo bởi hai cạnh đó. Công thức cụ thể là:

S = 1 / 2.a.b.sinC = 1 / 2a.c.sinB = 1 / 2.b.csinA

Ví dụ: Cho ABC là tam giác có cạnh AB: 5, BC: 7 và góc B 60 độ. Tính diện tích của tam giác trên.

Áp dụng công thức tính sau:

S = 1 / 2AB.BC.sinB = 1 / 2.7.5.sin60 = (35√3) / 4

Vì vậy diện tích của tam giác trên sẽ là (35√3) / 4.

• Tính diện tích của một tam giác có ba cạnh bằng công thức Heron

Khi biết cả ba cạnh, công thức tính diện tích tam giác như sau:

S = √p(p-a)(p-b)(p-c)

trong đó p được tính bằng công thức sau:

p = 1/2 (a + b + c)

Sau đó viết lại công thức tính diện tích tam giác như sau:

S = 1/4 (a + b + c) (a + b-c) (b + c-a) (a + c-b)

Ví dụ: Cho một tam giác có độ dài AB là 8, CB là 9 và AC là 7.

Áp dụng công thức, chúng tôi sẽ tính toán như sau:

Nửa chu vi của tam giác ABC là: p = (AB + BC + AC) / 2 = (8 + 9 + 7) / 2 = 12

• Diện tích của một tam giác theo công thức Herp như sau:

S = √p(p-AB)(p-BC)(p-AC) = √12(12-8)(12-9)(12-7) = 12√5

Vậy diện tích tam giác ABC là 12√5

• Tính diện tích tam giác theo bán kính bằng đường tròn ngoại tiếp

Công thức tính là:

S = (abc) / 4R

Trong đó: R là bán kính đường tròn ngoại tiếp tam giác.

Bạn cũng có thể sử dụng công thức sau:

S = 2R².sinA.SinB.SinC

Ví dụ: Cho tam giác ABC có độ dài các cạnh là a = 6, c = 5, b = 7, R, bán kính đường tròn ngoại tiếp tam giác ABC là 3. Tính diện tích hình tam giác.

Áp dụng công thức tính diện tích tam giác ABC như sau:

S = (abc) / 4R = (6.7.5) / (4.3√2) = 210 / 12√2 = 35√2 / 4

• Tính diện tích tam giác bằng bán kính của đường tròn nội tiếp

Công thức tính là:

S = p.r

trong đó: p là nửa chu vi của tam giác và r là bán kính của đường tròn nội tiếp.

Ví dụ: Cho ABC là tam giác có độ dài cạnh AB 20, cạnh BC 15, cạnh AC 21 và r 5.

Sau đó bạn áp dụng công thức tính chu vi hình tam giác sẽ được:

p = (AB + BC + AC) / 2 = (20 + 15 + 21) / 2 = 28

Diện tích tam giác ABC là:

S = p.r = 28.5 = 140.

Công thức diện tích tam giác đều

Định nghĩa

Tam giác đều là tam giác có 3 cạnh, 3 góc và 3 đường cao bằng nhau. Cả 3 góc đều là 60 độ.

Hình minh họa

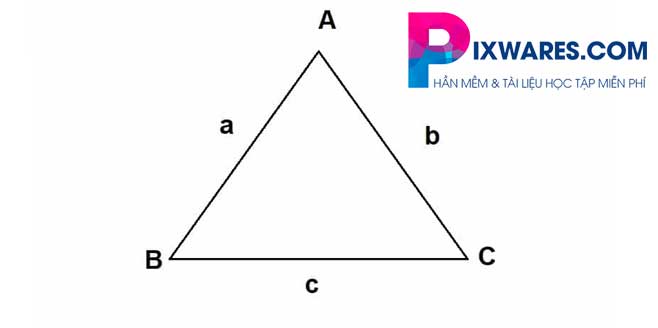
Công thức chu vi

Công thức tính chu vi hình tam giác đều là:

P = 3a

Công thức diện tích

Để tính diện tích của một tam giác đều, sử dụng công thức sau:

S = (a.h) / 2

Ví dụ
Cho ABC là tam giác đều cạnh 10 và chiều cao 5. Tính diện tích tam giác ABC.

Áp dụng công thức tính diện tích tam giác đều ABC ta sẽ được:

S = (10.5) / 2 = 25

Vậy diện tích tam giác vuông ABC là 25.

Công thức diện tích tam giác vuông

Định nghĩa

Tam giác vuông là tam giác có các góc bằng 90 độ. Trong góc vuông tại tam giác ABC và đỉnh B, a, b là độ dài hai cạnh của góc vuông. Sau đó các công thức tính chu vi và diện tích như sau:

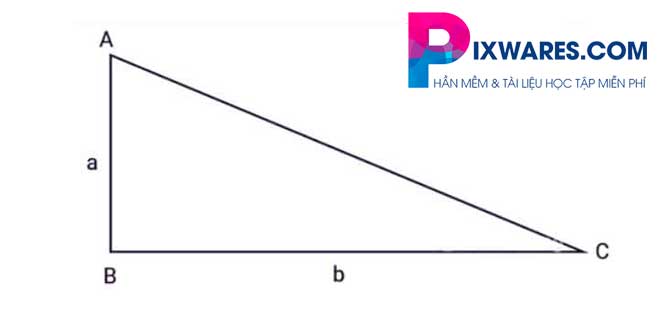
Công thức chu vi

Công thức tính chu vi tam giác vuông là:

P = a + b + c

Công thức diện tích

Công thức tính diện tích tam giác vuông là:

S = 1 / 2a.b

Ví dụ

Cho ABC là tam giác vuông tại góc B, cạnh BA là 5 cm và cạnh BC là 6 cm. Tính diện tích tam giác vuông ABC?

Áp dụng công thức tính diện tích tam giác vuông ABC như sau:

S = 1 / 2BA.BC = 1/2 (5.6) = 15 cm2.

Vậy diện tích tam giác vuông ABC là 15cm2.

Công thức diện tích của tam giác cân

Định nghĩa

Tam giác cân là tam giác có hai cạnh kề bằng nhau nên hai góc cũng bằng nhau. Trong tam giác ABC có ba cạnh, cạnh AB = AC, BC là đáy và ha là đường cao của tam giác từ đỉnh A đến đáy BC.

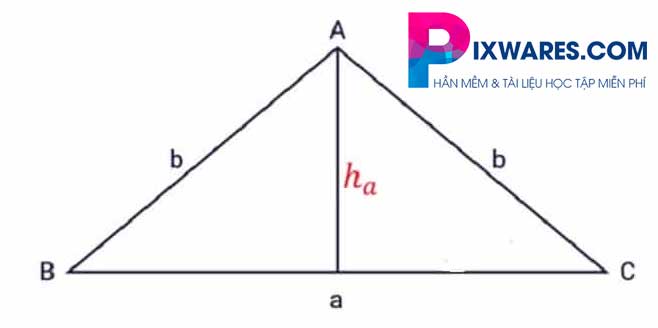
Công thức tính chu vi hình tam giác cân

P = a + b + c

Công thức tính diện tích tam giác cân như sau:

S = 1 / 2a.ha

Ví dụ:

Cho ABC là tam giác cân có đường cao từ đỉnh A đến BC là 7 cm và độ dài cạnh BC là 6 cm.

Khi đó diện tích tam giác cân ABC sẽ là:

S = (a.h) / 2 = (6.7) / 2 = 21 cm2.

Vậy diện tích tam giác cân ABC là 21cm2.

Công thức tính diện tích tam giác vuông cân

Định nghĩa

Tam giác vuông cân là tam giác có hai cạnh đồng dạng. Điều này làm cho 2 góc ở đáy bằng nhau và bằng 45 độ.

Với hình minh họa ở dưới, tam giác ABC là góc vuông cân, góc A bằng 90 độ, cạnh AB = AC như hình vẽ bên dưới:

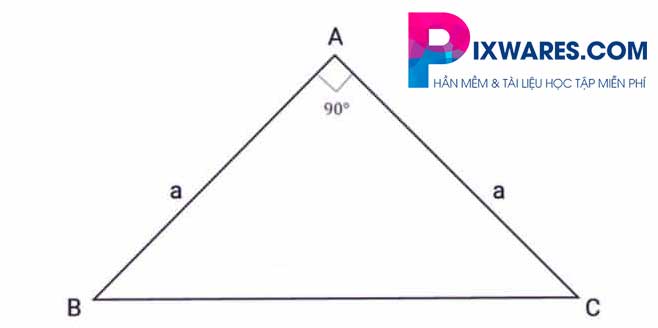
Công thức tính diện tích tam giác vuông cân là:

S = 1 / 2a²

Ví dụ

Cho ABC là tam giác vuông cân, đỉnh A cân và cạnh AC = AB = 8 cm. Tính diện tích tam giác vuông ABC.

Công thức tính diện tích tam giác cân ABC sẽ là:

S = 1 / 2a² = 1 / 2.8² = 32 cm2

Vậy diện tích tam giác vuông ABC là 32cm2

Cách tính diện tích tam giác trong hệ tọa độ Oxyz?

Nếu áp dụng công thức tính diện tích tam giác được chia sẻ ở trên, đối với không gian 3 chiều Oxyz thì bạn cũng được. Tuy nhiên, nó sẽ có rất nhiều khó khăn, vì vậy cách tốt nhất là bạn nên áp dụng công thức riêng của nó.

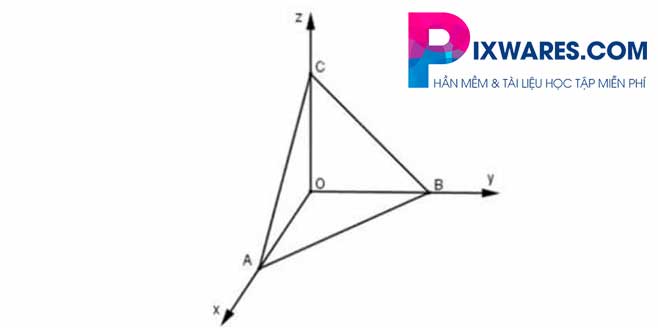
Công thức tính diện tích tam giác trong hệ tọa độ Oxyz như sau:

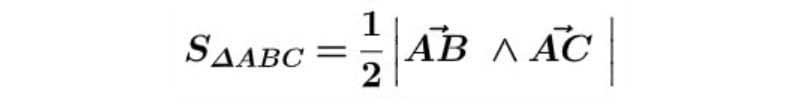
Ví dụ: Cho hệ trục tọa độ Oxyz và tam giác ABC có 3 đỉnh là A (-1; 1; 2), B (1; 2; 3), C (3; -2,0). Tính diện tích của tam giác trên.

Áp dụng công thức, ta sẽ được diện tích tam giác ABC trong hệ tọa độ Oxyz như sau:

S = 1/2 | AB∧AC | = 165/2